复杂度分析

占据数据结构和算法的半壁江山，是数据结构和算法学习的精髓。 数据结构和算法解决的是如何更快更省的存储和处理数据的问题。因此我们就要有一个考量效率和资源消耗的标准。这个就是复杂度分析方法

为啥需要复杂度分析

不用具体测试数据来测试，就可以粗略估计算法执行效率的方法，这就是时间，空间复杂度分析方法。所有代码的执行事件T(n)与每行代码的执行次数成正比
每一行都执行类似操作： 读数据-运算-写数据 T(n)=O(f(n))
T(n): 代码执行的时间
n： 数据规模大小
f(n):每行代码执行的次数总和
O ：代码执行时间T(n)和f(n)成正比

大 O 表示法：代码执行时间随数据规模增长的趋势。 当 n 很大的时候，就可以忽略并不左右的，例如变量，低阶，系数等，只关注最大的阶数就好

时间复杂度

时间复杂度，就是你代码运行的多少次 算法的执行时间与数据规模直接的增长关系。

1. 只关注循环次数最多的一段代码
2. 加法法则，总复杂度等于量级最大的那段代码的复杂度
3. 乘法法则，嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常见的时间复杂度实例分析

多项式量级

• 常量阶 O(1)
  常量级时间复杂度的表示方法，并不是只有一行代码 ，即便是有三行 diam ，时间复杂度也是O(1)
  一般情况下，算法中只要不出现循环语句，递归语句，即时有成千上万行代码，时间复杂度也是O(1)
• 对数阶 O(logn)
  不管是以 2 为底，还是以 3 为底，或者以 10 为底，我们把所有对数阶的时间复杂度记为O(logn)
  因为以 3 为底 n 的对数 =以 3 为底 2 的对数*以 2 为底 n 的对数，以 3 为底 2 的对数是一个常量，根据大 O 表示法，系数可以忽略，所以以 3 为底 n 的对数等于以 2 为底 n 的对数 而在对数的时间复杂度表示法中，我们通常忽略对数的底，故统一表示为O(logn)
• 线性对数阶 O(nlogn)
  如果一段代码的时间复杂度是O(logn),而这段代码又执行了 n 次，那么根据乘法法则，那么这段代码的时间复杂度就是O(nlogn)，是一种常用的算法时间复杂度，如归并，快排，时间复杂度都是O(nlogn)
• 线性阶 O(n)
• 平方阶 O(n^2), 立方阶 O(n^3)… K次方阶 O(n^k)
• O(n+m),O(n*m) 由两个数据规模决定的，

随着 n 的变大，他们几个的关系图如下

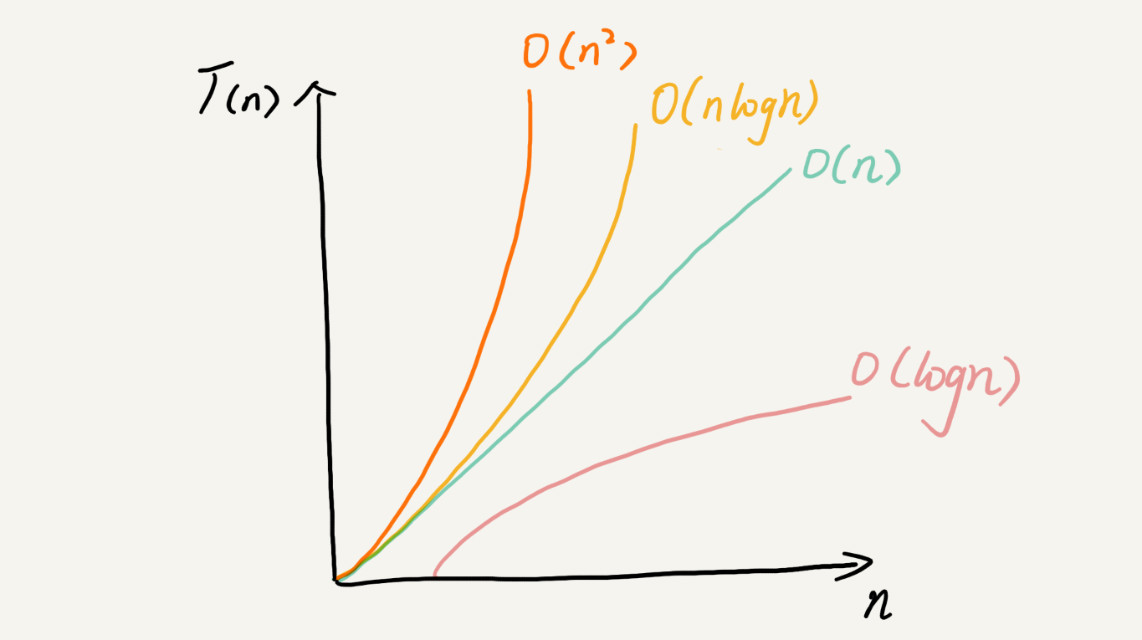
非多项式量级

当数据规模 n 越大，非多项式量级的算法的执行时间会急剧增加，求解问题执行时间就会无限变大，所以，非多项式时间复杂度的算法是一种非常低效的算法

• 指数阶 O(2^n)
• 阶乘阶 O(n!)

时间复杂度计算

for (int i = 0; i < n; i=i*2) {
    System.out.println(n);
}

假设循环次数是 t ，那么循环条件必须满足 2^t <n 即 t=log(2)(n) 以 2 为低 n 的指数。所以时间复杂度就是O(log(2)(n)),即时间复杂度是O(log(n)

什么是算法 举一个简单的例子

求和 ：1+2+3+…+n 方法一：

 for(i=1;i<n;i++){
   sum+=i;
 }

方法二 :

sum=n*(n+1)/2

这两个方法都能计算出来结果，并且都是正确的，但是方法一却很低效， n 越大，计算次数越多，时间复杂度是O(n)。 而方法二，就很高效，不管 n 是多少，只计算一次,即时间复杂度是O(1)，这就叫算法。

public int fib(int n){
      if(n==0||n==1){
          return 1;
      }
      return fib(n-1)+fib(n-2);
  }

递归类型，时间复杂度是O(2^n)

空间复杂度

算法的存储空间与数据规模直接的增长关系 常见的空间复杂度O(1),O(n),O(n^2),像O(logn),O(nlogn),这些一般都用不到。
指的是除了原本的数据存储空间外，算法还需要额外的存储空间。

最好，最坏，平均，均摊时间复杂度

最好时间复杂度

在最理想情况下，执行这段代码的时间复杂度

最坏时间复杂度

在最坏的情况下，执行这段代码的时间复杂度

平均时间复杂度

均摊时间复杂度